量子情報処理の諸分野の中でも最も実用に近いレベルにあるのは量子暗号である。現在のインターネットの世界で使われている暗号システムは公開鍵暗号方式と呼ばれ,大きな数の素因数分解が困難(非常に時間がかかり,実際には解読不可能)であることを活用したセキュリティシステムである。公開鍵方式とは,暗号化するための鍵(秘密鍵)と復号化のための鍵(公開鍵)をペアで創製し,暗号通信するAliceとBobがそれぞれ秘密鍵と公開鍵を持つことを特徴としている(RSA方式)。それぞれの鍵の長さは現在1028ビット(10進数で300桁)であり,この鍵の長さが長ければ長いほど暗号は強固である。ちなみに,1999年にRSA暗号で155桁(512ビット)の10進数の因数分解に292台のコンピュータで7.5ヶ月かかったとの報告があり,300桁はまず安全であると見なされている。しかし,量子コンピュータの章にて詳細は述べるが,1994年,AT&Tのショアは,量子コンピュータを使えば非常に高速に素因数分解が可能であることを示し,そのためのアルゴリズムをIEEEに発表した。ショアによれば,300桁の10進数の因数分解はわずか数分で完了してしまう。すなわち,現状の暗号システムは,量子コンピュータの実用化に伴い,いずれ崩壊することとなるのである(量子コンピュータの研究はショアのこの論文により著しく加速されたが,実用化は21世紀の半ば以降であろうと予測されており,当面RSA方式は健在である)。
RSA方式では,公開鍵を必要な人に配布する必要がある。問題なのは配布する過程における鍵の漏洩・紛失・盗難である。量子暗号システムは,暗号化のための鍵の配布をネットワーク上で行い,一度使用したら破棄する(One Time Pad方式)ことで秘密を保持することを特徴とする。鍵自体の創製はRSA方式のような複雑なロジックは必要ではなく,例えば,XOR(Exclusive OR)をとるためのビット列を2者間で共有するような,共通鍵方式で十分である。課題はネットワーク上での盗聴(Eavesdropping)だが,それを量子力学の基本原理である「観測は量子系の状態を撹乱する」ことを利用し,鍵の盗聴が無い時のみ暗号化通信を行うことで解決する。このような方式を量子暗号鍵配布(QKD;Quantum Key Distribution)方式と呼び,1984年にベネットとブラサードによって初めて基本方式が提案され,BB84プロトコル(規約)と呼ばれている。
[1]QKDの基本原理
1983年,ウイーズナーは量子論的な光の偏光状態を用いて,2つの異なるメッセージを安全に伝送する方法を提案した。まず2つのメッセージを両方とも2進数で表しておき,一方のメッセージについては,互いに直角な2つの直線偏光状態|V>と|H>で,もう一つのメッセージは右回り・左回りの円偏光状態|R>と|L>を用いて0と1の値を表し,光導波路に伝送する(|R> = {|V> + i|H>}/√2, |L> = {|V> - i|H>}/√2)のような重ね合わせの関係がある)。更に,メッセージの伝送の度毎に,2つのメッセージのうち,どちらを伝送するのかをランダムに選び出すようにしておく。このようにすれば,受信者は,偏光の性質から2つのメッセージのうちの片方は読み出せても,両方を正確に読み出すことはできない。これは次のような事情による。光の偏光方向を知るには,フィルターとなる物質に光を通せばよい。例えば,適当に切り出した方解石の結晶に光を入射すると,直進光と屈折光の2本の光が出力される。この2本の光は各々直線偏光状態にあり,その偏光方向は互いに直交している。従って,結晶から出力される光の出力位置によって,直線偏光を用いたメッセージは確実に読みとることができる。しかし,円偏光の光が方解石を通過すると,直線偏光状態の重ねあわせの状態が収縮して,直線偏光|V>か|H>のどちらかの状態が,ある確率をもって(完全な円偏光であれば,右回りであれ左回りであれ,|V>と|H>の出現確率はそれぞれ1/2)出現する。従って,右回りか左回りかの判定はできない。反対に,円偏光の向きを区別できるフィルターを用いると,直線偏光であることは失われて,右回りと左回りの円偏光状態がある確率で出現し,(|V> = {|R> + |L>}/√2, |H> = i{|R> - |L>}/√2)直進光か屈折光かの判断はつかない。受信者が片方のメッセージを解読できる装置を用意したとしても,両方のメッセージを正確に解読することは不可能である。2個のメッセージを繋ぎあわせて一つの意味のあるメッセージにしておくことにより,受信者(盗聴者)には安全な暗号メッセージとなる。
ウイーズナーの提案を契機として,暗号学に量子力学を用いる新しい流れが起こった。1984年,ベネットとブラサードはメッセージとしてOne Time Padの秘密鍵を送る方法を提案した。それはBB84プロトコルと呼ばれるQKDである。当初のBB84は光の偏光状態を使って表していたが,長距離通信には向かないことが判明し,現在では光の位相の性質を利用した装置が主流になってきている。この装置の心臓部にはマッハ・ツェンダー(Mach-Zehender;以下MZで表す)干渉計という,元来は,出力光の干渉縞から入力光の性質を精密に測定するための装置を用いている。MZ干渉計は以下のような原理で構成され,1個の入射光子のある偏光状態,例えば|0>から任意の重ね合わせ状態 ieiθ(sinδ/2*|0> + cosδ/2*|1>)を作り出すことができる。ここに,δは任意に設定できる。
[2]MZ干渉計
図1にMZ干渉計の構成を示す。
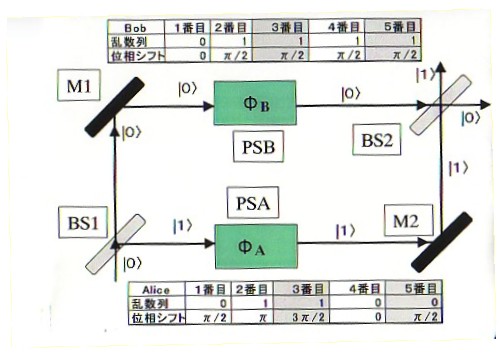
MZ干渉計は,
a.光を2方向に分ける2個のビームスピリッタ(BS1,BS2)
b.光の位相を変化させる2個の移相器(PSA,PSB)
c.光を全反射させる2枚の鏡(M1,M2)
からなり,光の入力・出力は各々2方向からなされる。その入力・出力ポートをそれぞれ(+),(-)で表し,(+)ポートからは量子状態|0>(偏光状態|V>, or |R>),(-)ポートからは量子状態|1>(偏光状態|H>, or |L>)が入るものとする。MZ干渉計の動作を,図1に示すように,量子状態|0>が下方から入った場合を使って説明する。
A.ビームスピリッタは2方向から入射された光を,反射・透過する機能を持つ。例えば,その割合を50%・50%の場合には特に,ハーフビームスピリッタと呼ばれ,量子状態|0>,|1>が通過後の状態を,
|0> → (|0> + i|1>)/√2
|1> → (|1> + i|0>)/√2
のように設定することができる。ハーフビームスピリッタは透過光の位相は変えないが,反射光は90度位相を変化させるからである。例では|0>が下方から入っているので,右方向に90度位相がずれて(虚数iがこれを表す)|1>成分が出力される。
B.移相器は,その名の如く任意の値だけ位相を変化させることができる。PSAを通過した後にφAだけ位相を変化させるとすると,|1>成分の位相がφA変化するので,
|0> → (|0> + ieiφA|1>)/√2
となる。一方,鏡M1の全反射では位相は変化しないので,PSBは|0>成分のみをφBだけ変化させる。従って,
|0> → (eiφB|0> + ieiφA|1>)/√2
= ei(φA + φB)/2*(ei(φB - φA)/2|0> + ie-i(φB - φA)/2|1>)/√2
がハーフビームスピリッタBS2への入力状態となる。結局,最終出力としては,
|0> → ei(φA + φB)/2*{ei(φB - φA)/2(|0> + i|1>)+ ie-i(φB - φA)/2(i|0> + |1>)}/2
= iei(φA + φB)/2*{sin(φB - φA)/2*|0> + cos(φB - φA)/2*|1>}
全体にかかる位相は量子状態には関与しないので,最終出力時に状態|0>,|1>が得られる確率はそれぞれ,sin(φB - φA)/2,cos(φB - φA)/2を2乗したものである。ここで重要なことは,この確率が位相差(φB - φA)/2のみに依存していることである。この位相差をδ= φB - φAとおき,δの値により秘密鍵を決定するのがBB84プロトコルである。以下,BB84について説明する。
[3]BB84プロトコル
通例に従って,送信者をAlice,受信者をBob,盗聴者をEveとする。量子論的な暗号鍵の配布とは,通信前には秘密情報を何も共有していないAliceとBobが0と1のランダムに並んだ数列(暗号鍵)をEveに知られずに共有することである。一旦暗号鍵を共有できれば,この鍵の長さと同一の長さの任意のメッセージ(ASCII形式等)を,鍵のビット列とXOR(Exclusive OR)をとってAliceは送信し,Bobは受信したメッセージを再度XORをとることで復号化できる。詳細手続きは以下の通りである。
(1)まずAliceは入力側の(+)ポートより偏光状態|0>の光子を1個入射する(実は,この1個というのが大変難しいのだが)。これはレーザ光を十分減衰させ,減衰させればさせただけ量子論的性質が浮き彫りになり盗聴行為は発見しやすくなる。Aliceはこのような光をある一定間隔,例えば300PS(100億分の3秒)ごとに発生させる。そして,AliceとBobはコンピュータを使って,上記MZ干渉計の移相器(PSA,PSB)を次のように独立に制御する。
(2)AliceとBobは0と1のランダムに並んだ数列を各自で作成する。この乱数列の長さは互いに揃えておく。例えばAliceは,「0,1,1,0,0,…」,Bobは「0,1,1,1,1,…」と作ったとする。
(3)Aliceは1個の光子を送る度に,自分の作成した乱数列に従って移相器PSAで位相を変化させる。乱数が0であれば,位相を0またはπ/2とし,1であれば位相をπまたは3π/2とする。(2)の例でいうと,例えば,「π/2,π,3π/2,0,π/2…」という順番で位相φAを設定したとする。
(4)Bobは,信号を受け取る直前に自分の作成した乱数列に従って移相器PSBで位相を変化させる。乱数が0であれば,位相を0とし,1であれば位相をπ/2とする。(2)の例でいうと,例えば,「0,π/2,π/2,π/2,π/2…」という順番で位相φBを設定したとする。
(5)Bobは自分のポートのどちらで光が出力されたかを記録しておく。(+)なら0,(-)なら1とする。Aliceが乱数列の内容をすべて送信し終わった後,お互いに設定した位相の情報を古典的通信方法(電話など)を使って確認し,Bobは位相差が0またはπのときの出力値のみを残す。上の例では3番目と5番目の時の出力値である。これを乱数列と見なし,暗号鍵とすればよい。位相差δが0またはπということは,Bobの側光の出力確率が0または1(sin0=0, cos0=1, sinπ/2=1, cosπ/2=0)を意味するからである。
この方式での安全性について考えてみる。Eveは単一パルスによる光レーザの技術に習熟しており,かつ任意の時間盗聴した光子の貯蔵が可能であるとする。この場合,Eveは(1)送信中の 光子を捉えて測定した後,測定結果と同種の光子をBobに送る,または(2)ビームスピリッタBSEを余分に光路中に置き,自分のほうにも出力されるようにしておく,ことが考えられるが,(1)の場合には光子の測定により,(2)の場合はBSEの設置により量子系の状態が変化してしまうことにより,Bobが受け取るデータの誤り率が大きくなってしまう。このことによりEveの存在が通信当事者に判明し,共通の暗号鍵が生成されなくなるのである。
以上がBB84によるQKDであるが,MZ干渉計を1セットしか用いていないため,送信者と受信者がそれぞれ遠距離にある場合の通信には向いていない。そこで考え出されたのがMZ干渉計を2セット用意し,干渉計の間を光ファイバーで結ぶか大気中を電波で飛ばすことにより通信する方法が1992年,ベネットにより提案された。この方式はB92プロトコルと呼ばれ,現在ではこの方法による実証実験が主流になってきており,100KM離れた場合でも通信が可能であることが証明されている。
(2002年4月14日;第一版 Copyright 寒泉)